Table of Contents
2013.03.14 - vector<> vs. list<>
almost exactly year ago Bjarne had a C++11 style presentation in Wrocław. aside from many interesting pieces of information, there was very nice example of how CPU caches and memory access affect applications' runtime, on modern hardware.
algorithm
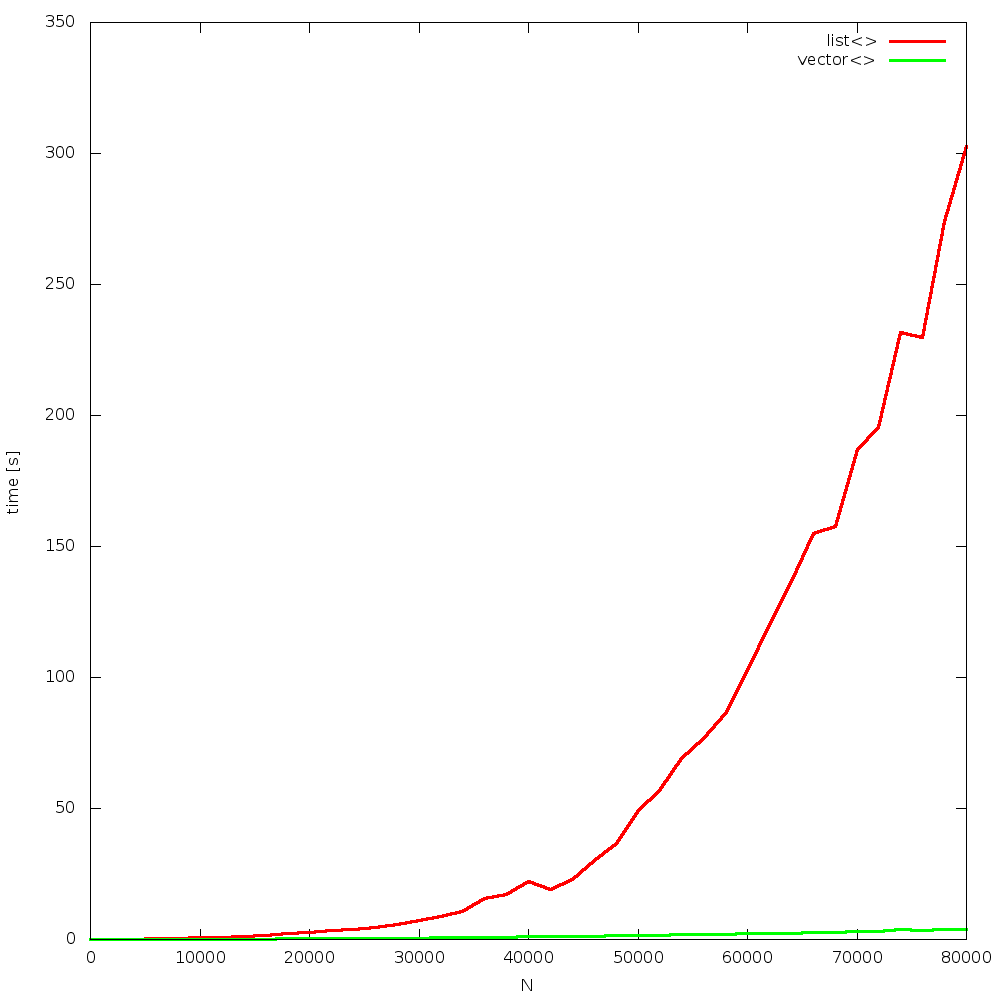
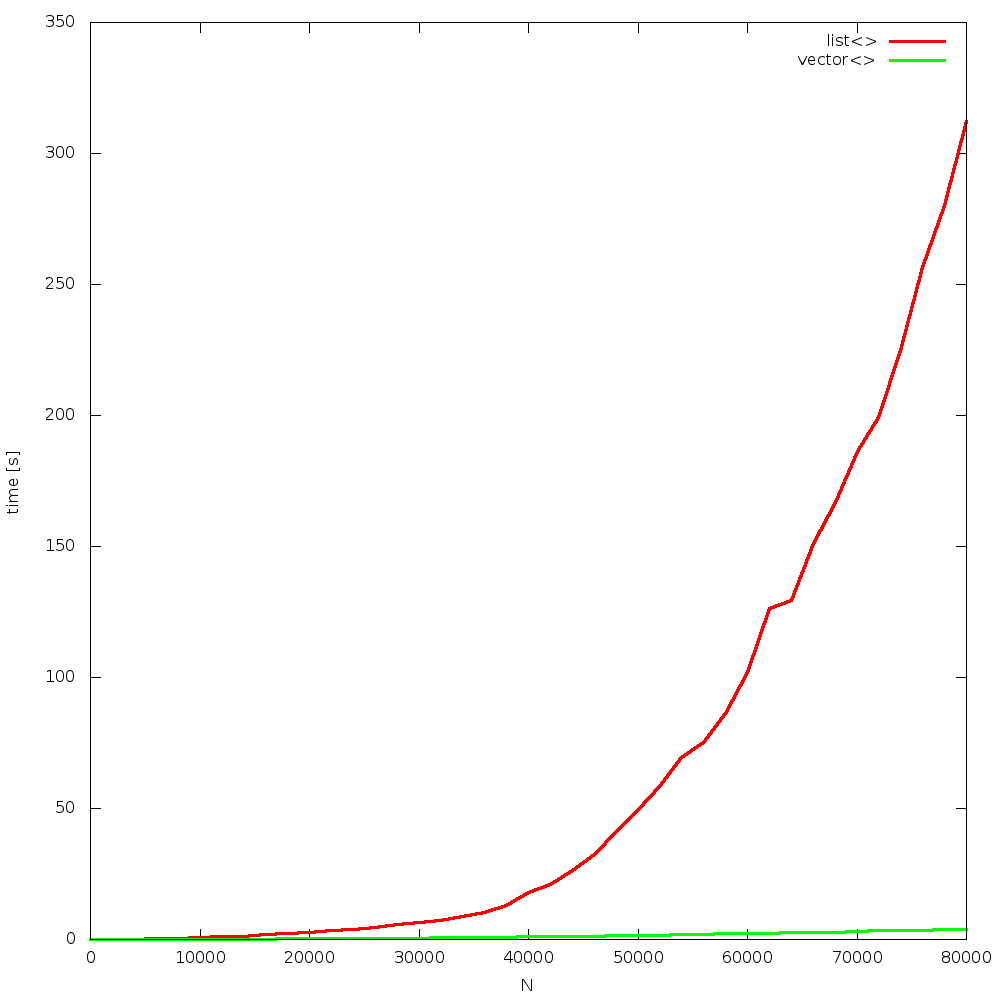
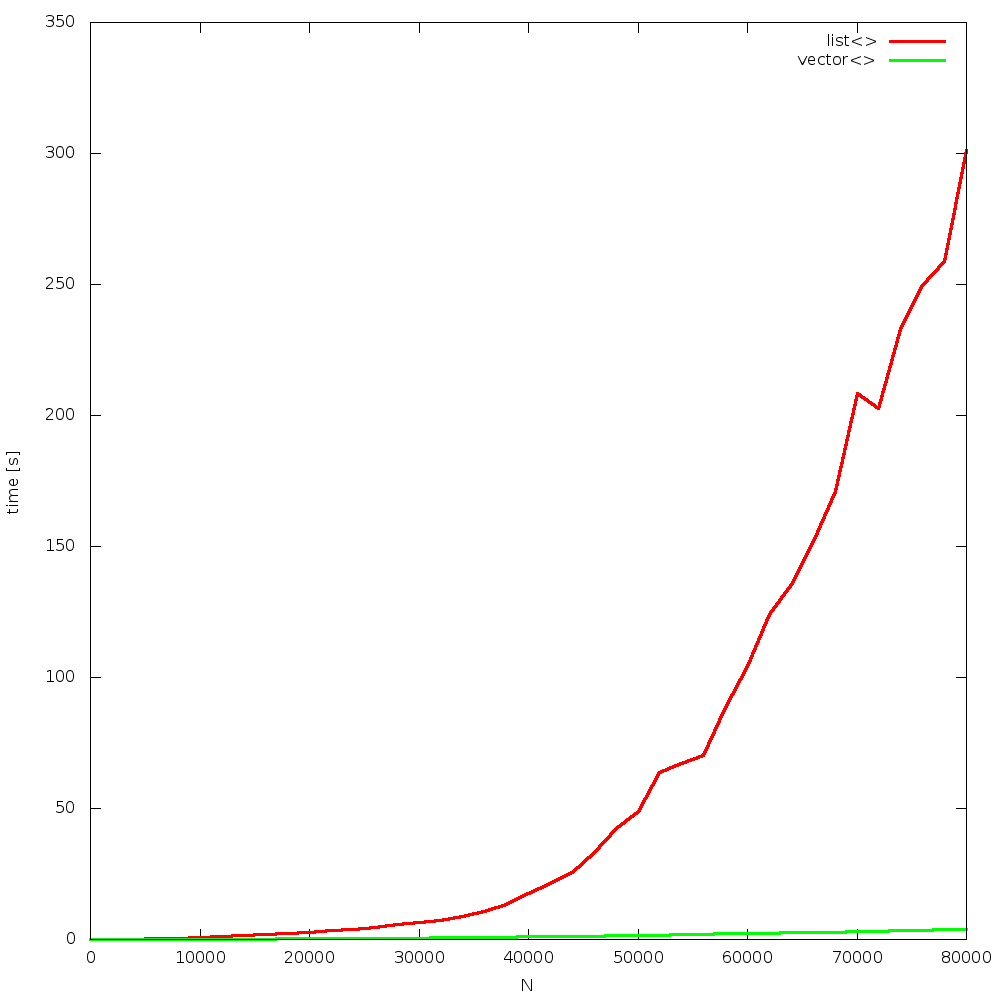
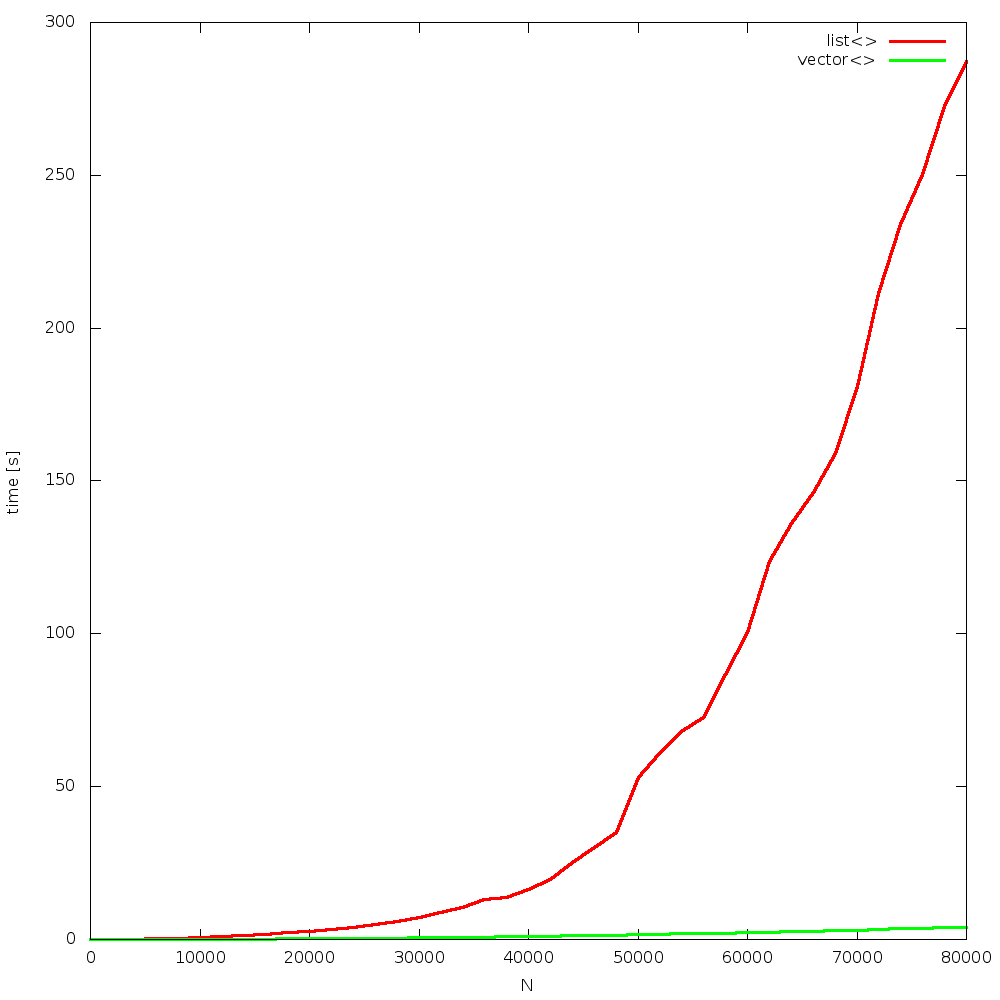
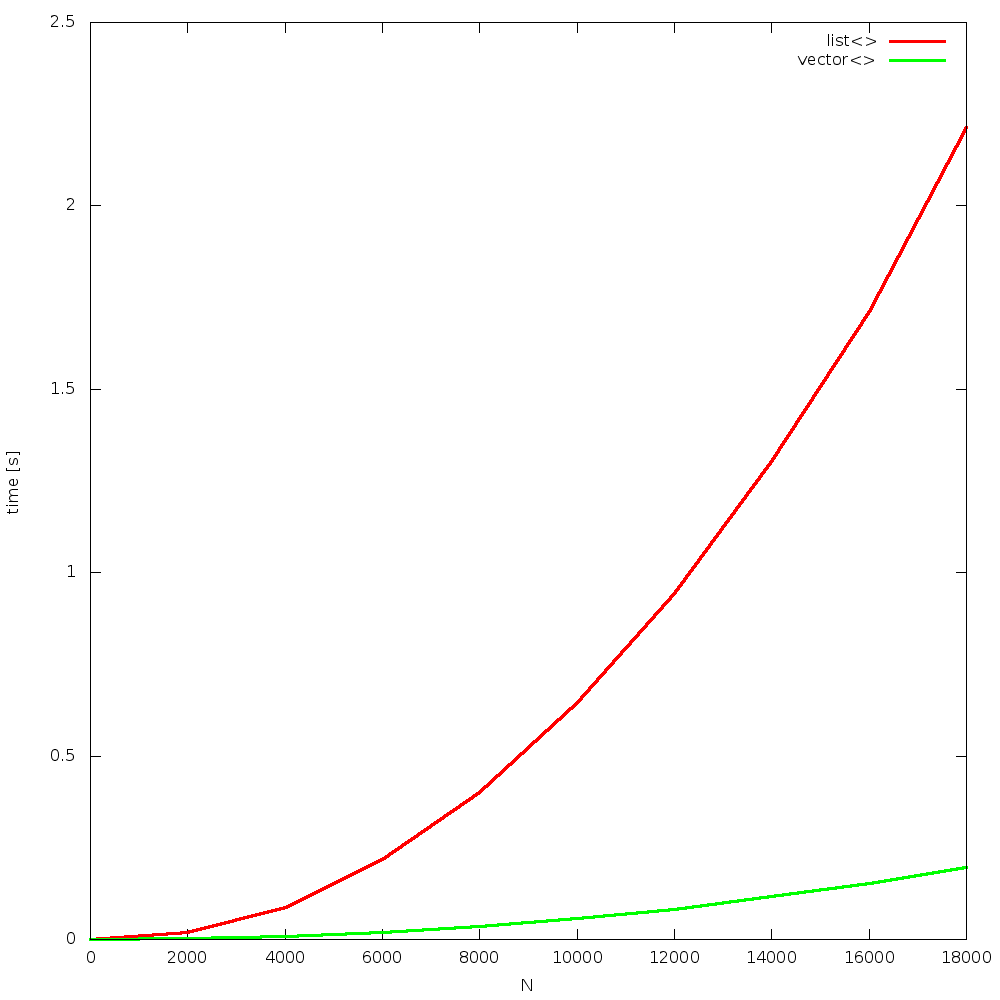
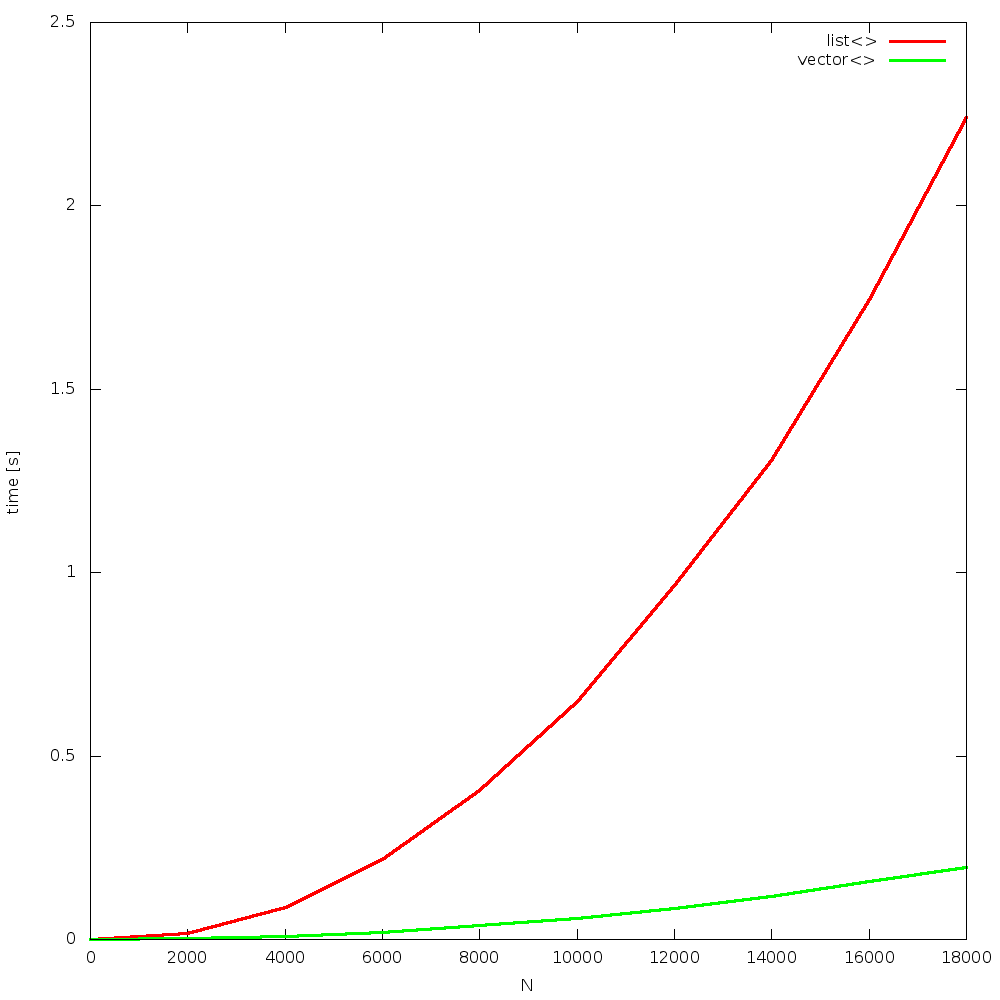
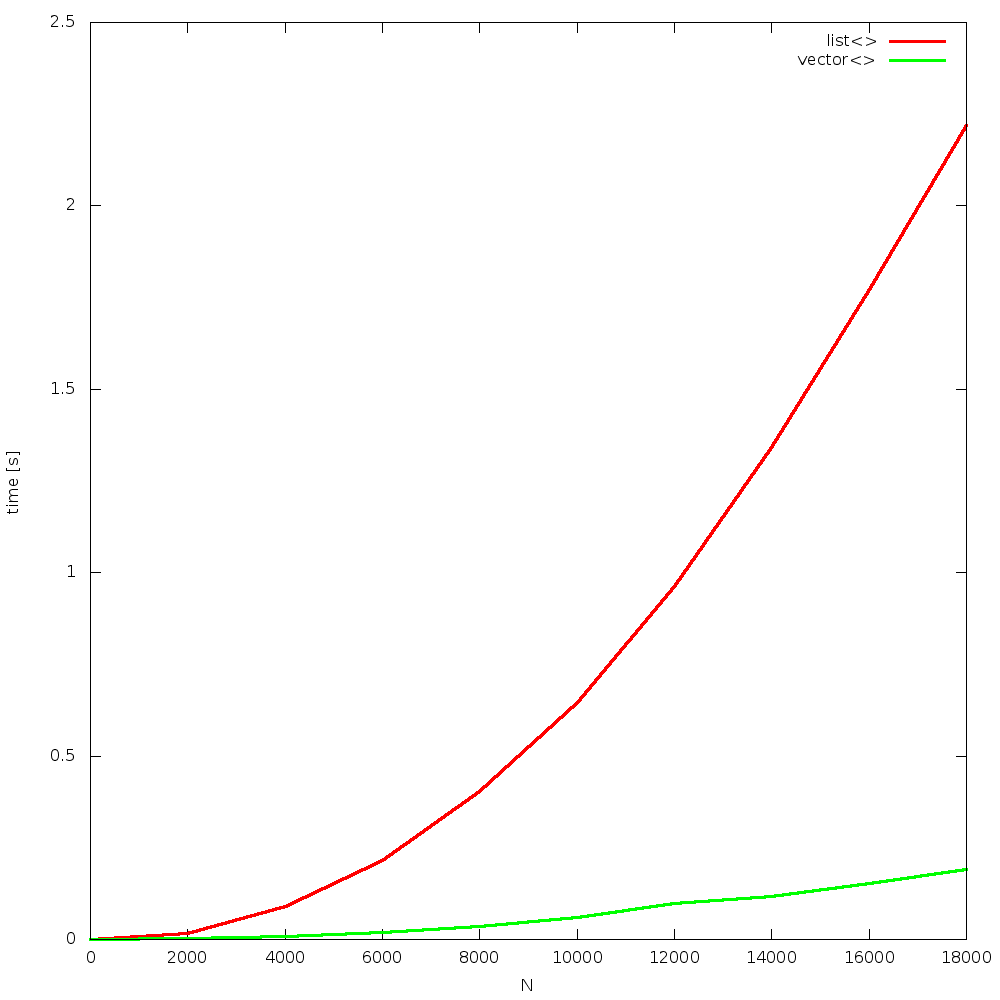
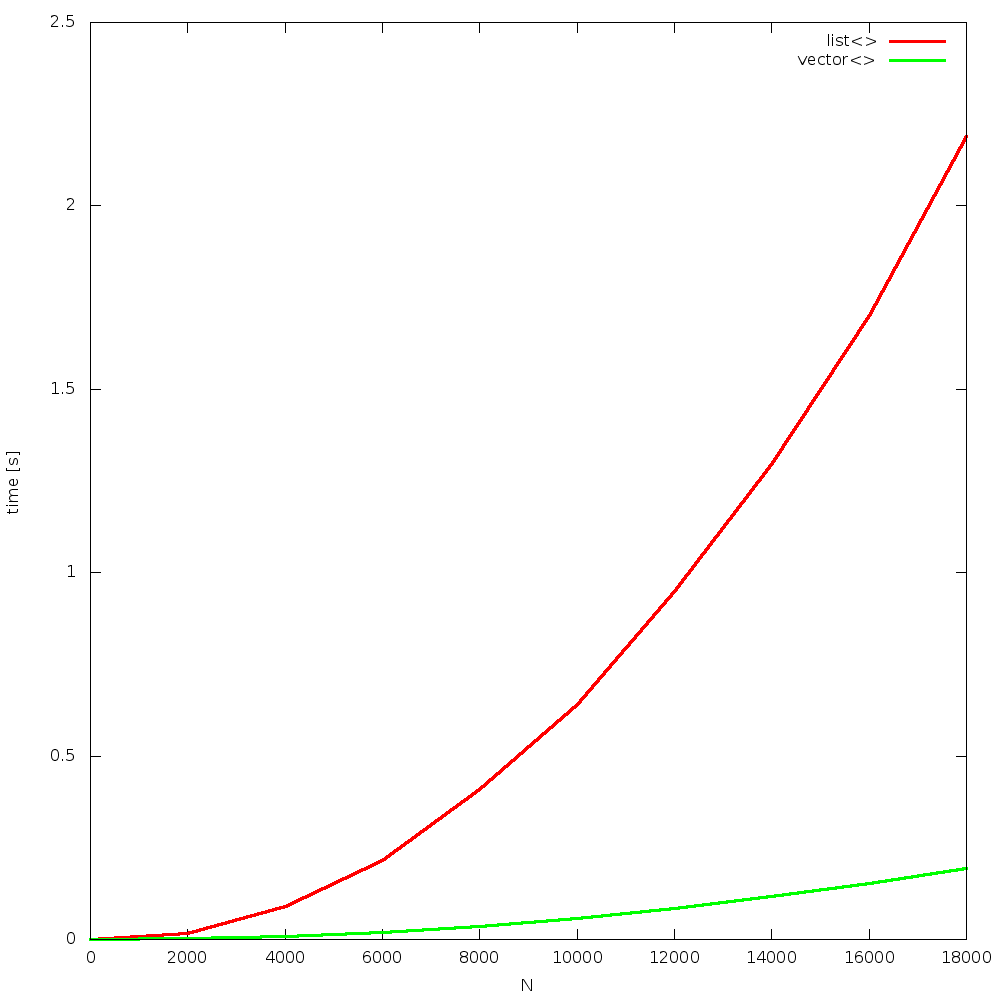
the algorithm is simple: insert N random elements to a container, so that it remains sorted all the time. after that, N times remove 1 element, from a random position. the question is: which container will be faster? list or vector? how big N will be the breaking point, where list is faster than vector? the answer is: never! due to constant cache misses, when using list, and constant cache hits, when using vector, the former one outperforms the other for all Ns!
recently i was doing a training/presentation, on cache and memory effects, for colleagues at work, and was not believed it is, as Bjarne suggested. “how come moving thousands of elements is faster than iteration over list nodes”? well it is. but of course we do not take anything on one's word – we do measure instead.
implementation
code implemented in C++, along with makefile for automatic generating images from gathered results, are available for download. for the reference, my test code follows:
// // implemented by BaSz @ 2013/q2 // // g++-4.7 -Wall -std=c++11 -O3 -DNDEBUG -march=native -o vector_vs_list.out vector_vs_list.cpp // #include <list> #include <vector> #include <chrono> #include <random> #include <iomanip> #include <iostream> #include <typeinfo> #include <algorithm> #include <cinttypes> #include <cassert> using namespace std; typedef chrono::high_resolution_clock Clock; typedef std::list<uint64_t> List; typedef std::vector<uint64_t> Vector; template<typename C, typename R> uint64_t algo(R r, const uint64_t n) { C c; typename C::value_type out = 0; // insertion for(uint64_t i=0; i<n; ++i) { const auto x = r(); auto it = c.begin(); while( it!=c.end() && *it<x ) ++it; c.insert(it, x); out+=x; } // sanity check assert( is_sorted( c.cbegin(), c.cend() ) ); // removal for(uint64_t i=0; i<n; ++i) { const auto pos = r() % c.size(); auto it = c.begin(); for(uint64_t i=0; i<pos; ++i) ++it; out+=*it; c.erase(it); } return out; } template<typename C> void run(const uint64_t n, const uint64_t seed) { // prepare rand mt19937 gen(seed); uniform_int_distribution<uint64_t> dist(0, n-1); auto r = [&]{ return dist(gen); }; // work auto start = Clock::now(); auto ret = algo<C>(r, n); auto stop = Clock::now(); // info auto diff = stop-start; cerr << typeid(C).name() << " = " << fixed << setprecision(3) << chrono::duration_cast<chrono::microseconds>(diff).count()/(1000*1000.0) << " [s] (xxx==" << ret%10 << ")\t"; } int main(void) { // initilize generator with some seed std::random_device rd; const auto initSeed = rd(); mt19937 gen(initSeed); cerr << ">> initial seed = " << initSeed << endl; for(uint64_t n=0; n<10*1000*1000l; n+=2000) { const auto seed = gen(); cerr << "N = " << n << "\t"; run<List> (n, seed); run<Vector>(n, seed); cerr << " \t (for seed " << seed << ")" << endl; } return 0; }
results
results were obtained from 4, random runs. figures are grouped in a “full” and “begin” sets. each run is presented on a separate figure. click on images to enlarge them.
full
begin
conclusion
Bjarne did not lie. this statement is true for over 10 years now. as CPUs become constantly way faster than memory, the gap increases over time.